O_一位全加器的Verilog设计
简介
全加器是能够计算低位进位的二进制加法电路。与半加器相比,全加器不只考虑本位计算结果是否有进位,也考虑上一位对本位的进位,可以把多个一位全加器级联后做成多位全加器。
一位全加器的数学表达式
- Sum=(A^B^Cin)
- Cout=(A·B)+Cin·(A^B)
- 其中A,B为要相加的数,Cin为进位输入;S为和,Co是进位输出。
真值表
| A | B | Cin | S | Cout |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
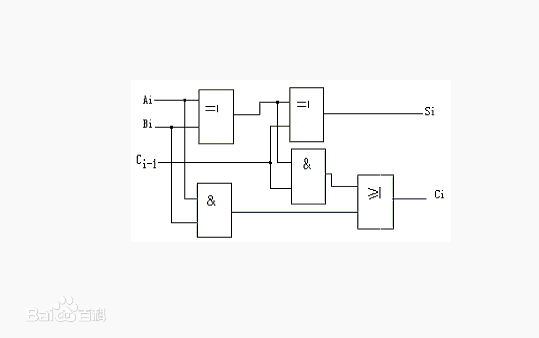
结构图(百度百科)
代码
module FullAdder(a,b,cin,s,cout);
input a,b,cin;
output s,cout;
wire t1,t2,t3;
xor(t1,a,b);
and(t2,a,b);
xor(s,t1,cin);
and(t3,t1,cin);
xor(cout,t3,t2);
endmodule
module Hatest;
reg A,B;
reg Cin;
wire S;
wire Cout;
FullAdder fa1(A,B,Cin,S,Cout);
initial
begin
A=1'b0;B=1'b0;Cin=1'b0;
#5 A=1'b0;B=1'b1;Cin=1'b0;
#5 A=1'b1;B=1'b0;Cin=1'b0;
#5 A=1'b1;B=1'b1;Cin=1'b0;
#5 A=1'b0;B=1'b0;Cin=1'b1;
#5 A=1'b0;B=1'b1;Cin=1'b1;
#5 A=1'b1;B=1'b0;Cin=1'b1;
#5 A=1'b1;B=1'b1;Cin=1'b1;
end
initial
$monitor($time,"A=%b,B=%b,Cin=%b---S=%b,Cout=%b",A,B,Cin,S,Cout);
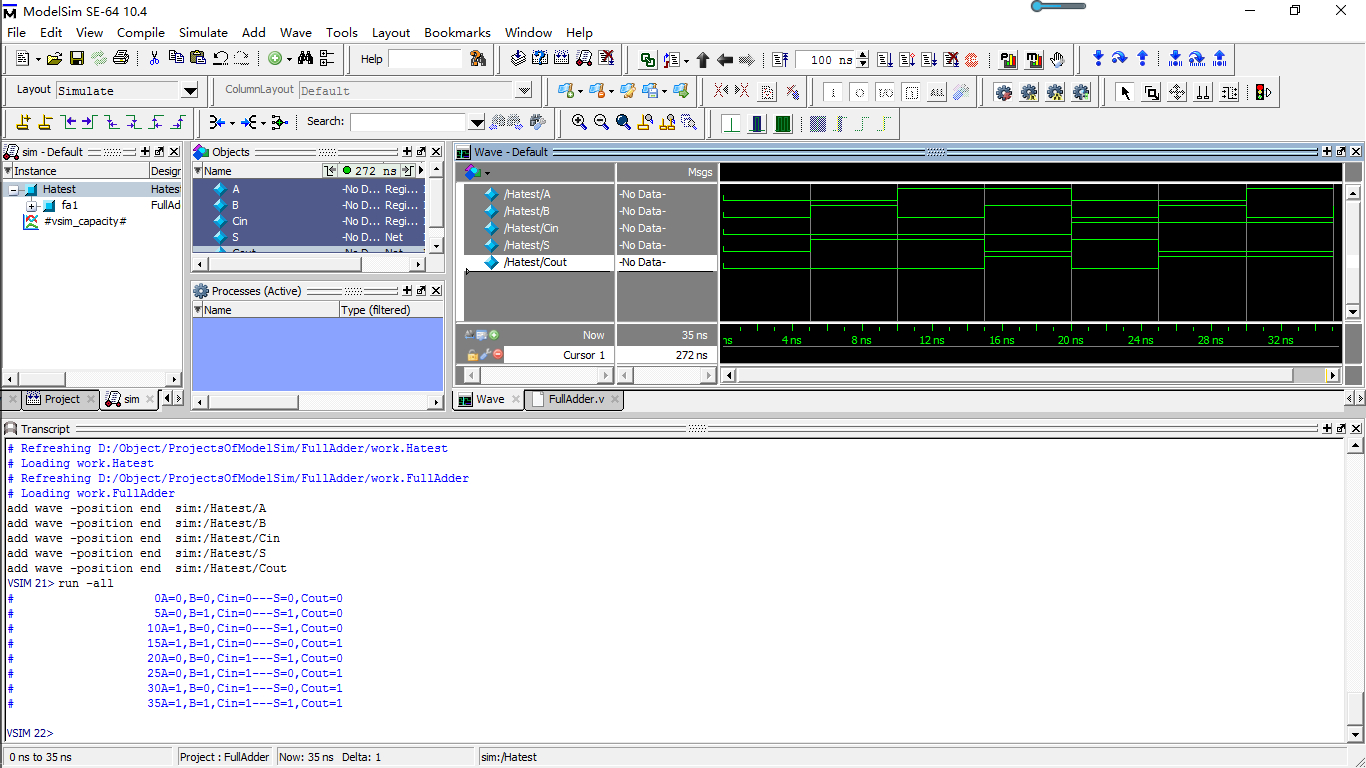
endmodule 波形及输出
评论已关闭